Diese Seite funktioniert nur mit Javascript.
Substitutionale Produktionsfunktionen, Isoquanten3.2.5 Grenzrate der technischen SubstitutionNiveauproduktionsfunktion, Skalenerträge
In Abbildung 1 beträgt sie für die Isoquante I2 im Punkt P -0,5. Wenn eine Einheit Arbeit weniger eingesetzt wird, kann die Produktion konstant gehalten werden, wenn im Gegenzug der Kapitaleinsatz um eine halbe Einheit ausgedehnt wird. Wenn eine Einheit Arbeit weniger eingesetzt wird, sinkt das Produktionsergebnis um die Grenzproduktivität der Arbeit. Zum Ausgleich wird in diesem Beispiel eine halbe Einheit Kapital benötigt, d. h. die Grenzproduktivität des Kapitals ist doppelt so hoch. Die Grenzrate der technischen Substitution entspricht dem (umgekehrten, negativen) Verhältnis der Grenzproduktivitäten der Faktoren.
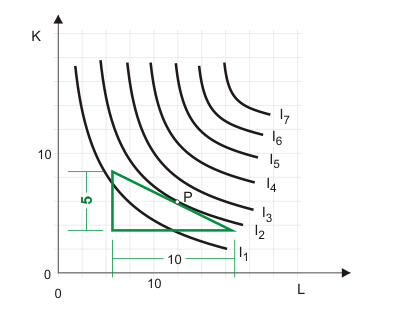
Man erkennt aus dem Verlauf der Indifferenzkurven in Abbildung 1 eine (absolut) abnehmende Grenzrate der technischen Substitution. Ähnlich wie in der Haushaltstheorie beim Gesetz von der abnehmenden Grenzrate der Substitution wird auch hier der konvexe Isoquantenverlauf als typisch erachtet und der abnehmenden Grenzrate der technischen Substitution eine Gesetzmäßigkeit zugesprochen. Ob im Einzelfall für einen Produktionsprozess das Gesetz von der abnehmenden Grenzrate der technischen Substitution gilt, hängt von den Grenzproduktivitäten der Faktoren ab. Die Zusammenhänge sind etwas komplex, da sich die Grenzproduktivitäten in der Regel auch gegenseitig beeinflussen. So steigt im allgemeinen die Grenzproduktivität der Arbeit, wenn sich der Kapitaleinsatz in der Produktion erhöht. Folgenden Spezialfall kann man aber in Gedanken nachvollziehen: Gelte für den Faktor Arbeit das Gesetz von der abnehmenden Grenzproduktivität und sei zugleich die Grenzproduktivität des Faktors Kapital konstant. Dann ist um so weniger Kapital zum Ersatz einer Arbeitseinheit notwendig, je mehr Arbeit im Produktionsprozess eingesetzt wird. Also gilt in diesem Fall das Gesetz von der abnehmenden Grenzrate der technischen Substitution.
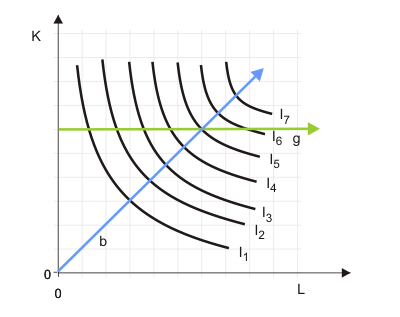
In Abbildung 2 werden zwei Bewegungen im Isoquantendiagramm betrachtet. Wenn man dem grünen Pfeil (g) folgend für jeden Punkt die Arbeitseinsatzmengen notiert und an den Isoquanten die Produktionsmenge abliest, erhält man eine Ertragskurve bei partieller Faktorvariation - die Ihnen bekannte "normale" Produktionsfunktion $x=f(L)$. Diese entspricht der grünen Kurve in der Abbildung des Produktionsgebirges. Wenn man sich auf der blauen Linie bewegt, wird der Einsatz beider Faktoren verändert, während die Relation zwischen ihnen konstant gehalten wird. Die Kapitalintensität bleibt also konstant. Die Bewegung entspricht der blauen Linie in der Abbildung des Produktionsgebirges. Da beide Faktoren variiert werden, handelt es sich um eine totale Faktorvariation. Die resultierende Ertragskurve heißt Niveauproduktionsfunktion. Sie wird im nächsten Abschnitt besprochen.